更好的代码
“好”的代码与“坏”的代码
虽然对于“什么是优秀的代码“难以形成一致意见,但是这么多年的经验,让我对代
码“好”与“坏”积累了一些自己的看法。
比如说,“好”的代码应该:
1.容易理解;
2.没有明显的安全问题:
3.能够满足最关键的需求;
4.有充分的注释:
5.使用规范的命名;
6.经过充分的测试。
“坏”的代码包括:
1.难以阅读的代码:
2.浪费大量计算机资源的代码:
3.代码风格混乱的代码:
4.复杂的、不直观的代码:
5.没有经过适当测试的代码。


这种阅读起来的确定性至少有三点好处,第一点是可以减少代码错误;第二点是可以节省我思考的时间;第三点是可以节省代码阅读者的时间。
减少错误、节省时间,是我们现在选择编码方式的一个最基本的原则。
快速排序
两个考察点:分治、双指针实现快速partition
时间复杂度:
平均 lgn;
最坏:n^2
最好:
1 | //快速排序算法模板 |
对于有序数组,上面把start作为Pivot的方法,会让算法时间复杂度退化为O(N^2),导致超时。
对数组进行shuffle,能解决有序数组的问题,但是无法解决所有元素全部相同的问题。当所有元素都一样时,shuffle无用,时间复杂度还是O(N^2)
于是就有了下面的解法。这种方法,返回了中间区域的左右边界,让问题迅速简化!
1 |
|
贪心-分糖果问题
一群孩子做游戏,现在请你根据游戏得分来发糖果,要求如下:
- 每个孩子不管得分多少,起码分到一个糖果。
- 任意两个相邻的孩子之间,得分较多的孩子必须拿多一些糖果。(若相同则无此限制)
给定一个数组 arrarr 代表得分数组,请返回最少需要多少糖果。
要求: 时间复杂度为 O(n)O(n) 空间复杂度为 O(n)O(n)
1 |
|
链表系列-删除重复节点
1 | /** |
回溯-N皇后问题
状态:已经填好的行数,每一行填在了哪些位置
选择: 最多N种选择
路径:放置了Queue的
结果集:列表的列表
结束条件: 已经把所有的行数填写完;
1 | class Solution { |
计算机排序算法
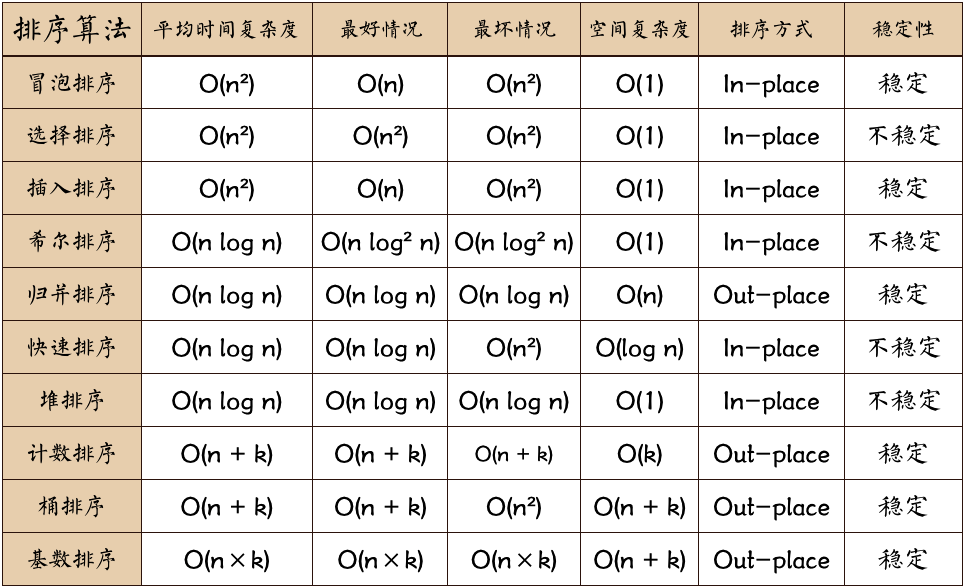
outplace的都是稳定的;
outplace的需要一定的memory, inplace中的qsort由于是递归的,所有需要lgn的mem,其他的都不要额外的内存
inplace大多数都不稳定,除了冒泡排序、插入排序
| 算法 | 思想 | 衍生问题 |
|---|---|---|
| quick sort | 分治思想,借助双指针在$O(n)$时间内完成partition | 线性第k大,线性求中位数 |
| merge sort | 分治思想,双指针(稳定的) | 逆序数 |
| heap sort | 借助容器来实现排序,还有类似的BST中序遍历 | topK问题 |
| counting sort | 空间换时间,非比较;通过扫描min/max来支持负数,通过累加和+倒序遍历来保持稳定 | |
| bucket sort | 抽屉原理,稳定排序,适合元素值集合较小的情况,特别适合外部排序 | 排序后最大间隔问题、大整数文件取中位数问题 |
| radix sort | 稳定子排序算法(计数排序、桶排序来实现)对数字进行k遍排序 | |
| shell sort | 分块思想,缩小增量排序,一种特殊的插入排序;递减序列的选择很重要 | 适用于基本有序序列 |
| insertion sort | 减治思想,扑克牌 | 适用于基本有序序列 |
| Bubble sort | 稳定 |
归并排序
归并排序,是一种特别有用的排序算法;
它背后的算法思想是 分治。
归并排序同时也是一种思想,可以解决归并排序思想解决很多问题。
例如,计算逆序数。
1 | //归并排序算法模板 |
高性能服务器系列-线程池
核心参数
1、corePoolSize:线程池中的常驻核心线程数
2、maximumPoolSize:线程池能容纳同时执行的最大线程数,此值必须>=1
3、keepAliveTime:多余的空闲线程的存活时间
当前线程池数量超过corePoolSize时,当空闲的时间达到keepAliveTime值时,多余的空闲线程会被直接销毁直到只剩下corePoolSize个线程为止
4、timeUtile:keepAliveTime的单位
5、workQueue:任务队列,被提交但未被执行的任务
6、threadFactory:表示生成线程池中工作线程的线程工厂,用于创建线程一般用默认的即可。
7、handler:拒绝策略,表示当队列满了并且工作线程大于等于线程池的最大线程数
工作流程
线程池内部是通过队列+线程实现的,当我们利⽤线程池执⾏任务时:
- 如果此时线程池中的线程数量⼩于corePoolSize,即使线程池中的线程都处于空闲状态,也要创建
新的线程来处理被添加的任务。 - 如果此时线程池中的线程数量等于corePoolSize,但是缓冲队列workQueue未满,那么任务被放⼊
缓冲队列。 - 如果此时线程池中的线程数量⼤于等于corePoolSize,缓冲队列workQueue满,并且线程池中的数
量⼩于maximumPoolSize,建新的线程来处理被添加的任务。 - 如果此时线程池中的线程数量⼤于corePoolSize,缓冲队列workQueue满,并且线程池中的数量等
于maximumPoolSize,那么通过 handler所指定的策略来处理此任务。 - 当线程池中的线程数量⼤于 corePoolSize时,如果某线程空闲时间超过keepAliveTime,线程将被
终⽌。这样,线程池可以动态的调整池中的线程数
合理线程数
CPU密集型:CPU核数+1个线程的线程池
IO密集型:a)CPU核数*2;b)CPU核数/(1-阻塞系数)。(阻塞系数:0.8~0.9)
拒绝策略
第一种拒绝策略是 AbortPolicy,这种拒绝策略在拒绝任务时,会直接抛出异常 RejectedExecutionException (属于RuntimeException),让你感知到任务被拒绝了,于是你便可以根据业务逻辑选择重试或者放弃提交等策略。
第二种拒绝策略是 DiscardPolicy,这种拒绝策略正如它的名字所描述的一样,当新任务被提交后直接被丢弃掉,也不会给你任何的通知,相对而言存在一定的风险,因为我们提交的时候根本不知道这个任务会被丢弃,可能造成数据丢失。
第三种拒绝策略是 DiscardOldestPolicy,如果线程池没被关闭且没有能力执行,则会丢弃任务队列中的头结点,通常是存活时间最长的任务,这种策略与第二种不同之处在于它丢弃的不是最新提交的,而是队列中存活时间最长的,这样就可以腾出空间给新提交的任务,但同理它也存在一定的数据丢失风险。
第四种拒绝策略是 CallerRunsPolicy,相对而言它就比较完善了,当有新任务提交后,如果线程池没被关闭且没有能力执行,则把这个任务交于提交任务的线程执行,也就是谁提交任务,谁就负责执行任务。这样做主要有两点好处。
第一点新提交的任务不会被丢弃,这样也就不会造成业务损失。
第二点好处是,由于谁提交任务谁就要负责执行任务,这样提交任务的线程就得负责执行任务,而执行任务又是比较耗时的,在这段期间,提交任务的线程被占用,也就不会再提交新的任务,减缓了任务提交的速度,相当于是一个负反馈。在此期间,线程池中的线程也可以充分利用这段时间来执行掉一部分任务,腾出一定的空间,相当于是给了线程池一定的缓冲期。
用户增长
用户增长的前提是你的产品是满足需求的,且与市场是匹配的(用户来了之后才能够留得住),但到达用户存在阻碍。
所以用户增长的主要工作就是:要减少阻碍,降低交易成本(比如认知成本、信任成本、分享成本等等)。
开始前,先问问自己 7 个与增长相关的基础问题,带着问题思考更高效。
(1)XX公司的商业模式是什么?
(2)XX公司所在的社会环境是什么?
(3)XX公司处在企业生命周期的什么阶段?
(4)XX公司的增长战略、增长策略、增长战术是什么?
(5)XX公司的用户是谁?
(6)XX公司当前是怎么做用户增长?
(7)XX公司的北极星指标是什么?
(因为)不同商业模式、不同阶段,则有不同的增长侧重。所以谈用户增长不能不谈商业模式、社会大环境、企业生命周期。