$Y = \theta * X + \epsilon $
我们现在的目标是找到一组$\theta$可以让它乘以X之后尽可能的匹配Y
$\epsilon$为误差,服从均值为0,方差为$\mu^2$的正态分布
预测值与真实值之间有误差
学习的关键在于:确定什么样的参数最符合于你的目标
我们的目标是什么? 让误差项尽可能的小,接近于0,loss函数等于0
条件概率: 也服从正态分布。
对于某一个样本,要找到一个theta, 跟x组合之后,成为真实值y的可能性最大
从误差的正态分布得到

上图啥意思呢?上图最后得到了一个概率密度函数,表示在$\theta$,跟$x^{(i)}$组合之后得到$y^{(i)}$的可能性(也就是概率)
最大似然函数
上面的概率函数,通俗来讲“要找到一个$\theta$,跟$x^{(i)}$组合之后,成为$y^{(i)}$的可能性,越大越好”
假设去了赌场(赌场中有一个固定的暗箱操作套路$\theta$),我们现在尝试去猜测这种套路?
来了一个人,我们按照这个套路去猜,猜对了,概率很高;
又来了一个人,我们还是按照这个套路取材,猜对了,概率也很高…
最有,我观察的人足够多之后,我们才敢宣称,我猜对了赌场的套路。
同样的,我们需要找到一组参数,匹配所有样本的概率尽可能的大,也就是说下面的概率最大
$p(y^{(1)},y^{(2)},…,y^{(n)}|\theta;x^{(1)},x^{(2)},…,x^{(n)})$
那么这个概率是多少呢?
又因为每一个样本的误差都是独立同分布的,所以联合概率等于每一个边缘概率的乘积,也就说:
也就是下面的公式

有了上面的累乘之后呢?我们如何求解到一个合适的$\theta$让上面的概率最大呢?不太容易,因为是乘法。
【启发思考】对于乘法,我们一般会取log,将其转换为加法,也就变成了上图中的“对数似然函数”
最小二乘法为啥可以作为线性回归的损失函数

如上图,我们对对数似然函数进行化简得到一个结论,我们想要对数似然函数最大,等价于让$J(\theta)$最小;这也就是我们通常听到的“最小二乘法”,也就是线性规划算法的目标函数
最优化常用解法之-梯度下降
最优化问题有很多解法,我们这里先介绍最常见的梯度下降算法【Gradient Descent】

梯度,就是函数的导数。如果自变量有多个,我们就针对每一个自变量($\theta_1,\theta_0$)求偏导。
求导时,你可能需要知道的求导链式法则。
对于要迭代的每一步执行以下步骤:
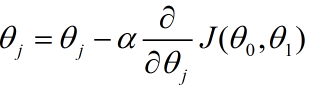
学习率太高,步子迈得太大,容易跑偏,从而错过极值点;学习率太低,步子过小,算法收敛的会特别慢,程序运行会比较慢。
- 批量梯度下降
- 随机梯度下降
- miniBatch梯度下降
参考:https://www.bilibili.com/video/BV1uM411r7Cv?p=4&vd_source=9a48b33279c3ad3689807d049311d0ee

