Neo's Blog

不抽象就无法深入思考
不还原就看不到本来面目!

0%

Posted on Edited on In Valine:

题目描述

假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

  1. 你可以多次买卖该只股票，但是再次购买前必须卖出之前的股票
  2. 如果不能获取收益，请返回0
  3. 假设买入卖出均无手续费

思路

我是上帝，要想利润最大，就是吃到所有的波段！低买高卖！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        if (prices.empty()) {
            return res;
        }
        for (int i = 1; i < prices.size(); ++i) {
            if (prices[i] > prices[i - 1]) {
                res += prices[i] - prices[i - 1];
            } 
        }

        return res;
    }
};

Posted on Edited on In Valine:

给出一个长度为 n 的，仅包含字符 ‘(‘ 和 ‘)’ 的字符串，计算最长的格式正确的括号子串的长度。

例1: 对于字符串 “(()” 来说，最长的格式正确的子串是 “()” ，长度为 2 .
例2：对于字符串 “)()())” , 来说, 最长的格式正确的子串是 “()()” ，长度为 4 .

Read more »

Posted on Edited on In Valine:

题目描述

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0到n-1之内。

在范围0到n-1的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

样例
输入：[0,1,2,4]

输出：3

实现思路

根据题目描述容易得到：如果把miss的数字补齐，那么我们可以得到序列：$1,2,3,…n$

递增，数组，容易想到是否可以用二分查找。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
   int getMissingNumber(vector<int>& nums) {
        int n = nums.size();
        int sum = 0;
        for (auto x: nums) {
            sum += x;
        }  
        return (n * (n + 1) >> 1) - sum;
    }
};

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int j = nums.size();
        int i = 0;
        while (i < j) {
            int  m = (i + j) >> 1;
            if (m < nums.size() && nums[m] == m) { //如果是合法的，说明需要往后find.
                i = m + 1;
            } else {
                j = m;
            }
        }
        
        return i;
    }
};

相关题目

寻找重复

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，找出 这个重复的数 。

1.不能更改原数组（假设数组是只读的）。
2.只能使用额外的 O(1) 的空间。
3.时间复杂度小于 O(n2) 。
4.数组中只有一个重复的数字，但它可能不止重复出现一次

思路：

该题目约束比较多，不能更改原数组，意味着不可以使用数组自hash或者原地交换；

限制了空间，意味着不可以使用某些排序算法或者使用hash map。

可以选择的时间复杂度: $O(n)$、$O(n * lgn)$

可以考虑二分，二分的话有两种：二分数组、二分答案

显然我们的数组并没有排序，所以更有可以是二分答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution
public: 
    int findDuplicate(vectorzint>&nums){
    int n=nums.size();
    int l=1,r=n-1,ans=-1;
    while(l<=r)
    {
            int mid=(l+r)/2;int cnt=0;
            for(int i=0;i<n;i++){
                cnt=cnt+(nums [i]<=mid)
            }
            if(cnt<=mid)
                l=mid+1;
            else {
                r=mid-1;
                ans=mid
            }
    }
    return ans
}

Posted on Edited on Valine:

寻找数组局部最小值

解答思路：

只要有最小值，那我就可以找到。

a[0] <= a[1], 则a0就是极小值；
a[n - 2] >= a[n - 1], 则a[n-1]就是极小值

否则，就如图(一定有最小值）：

Posted on Edited on Valine:

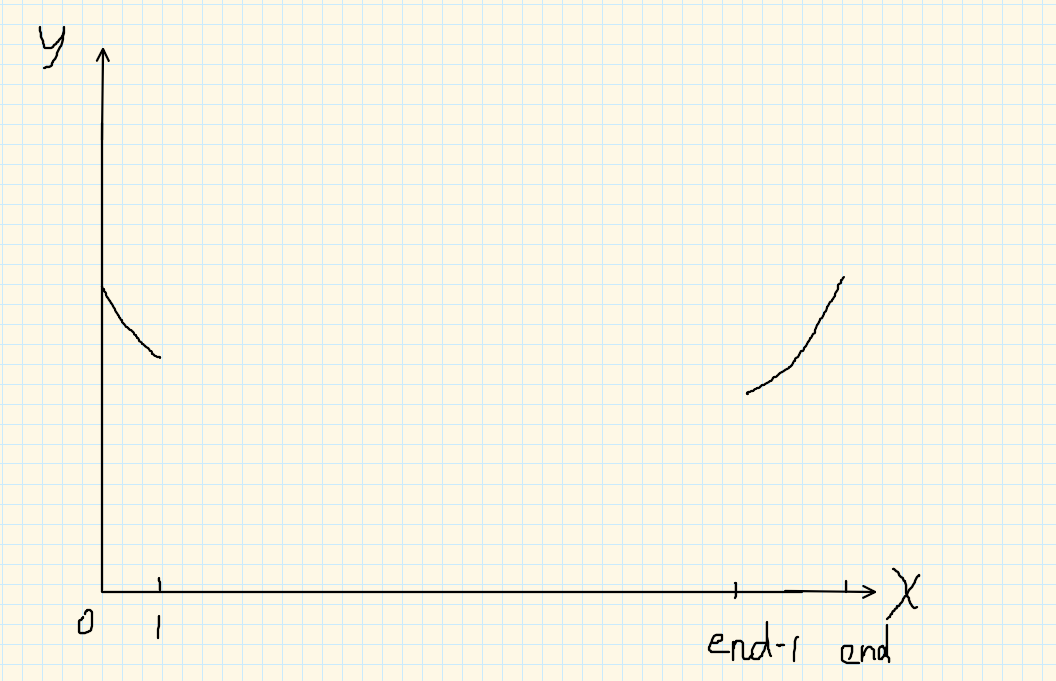
两个集合的交集

（1）排序 + 双指针
（2）hashmap + counter

如果内存放不下如何办？

通过归并外排将两个数组排序后再使用排序双指针查找

最终，集合1和集合2的交集，是x与y与z的并集，即集合{3,5,7,30,50,70}。

画外音：多线程、水平切分都是常见的优化手段。

skiplist 跳表来维护有序结构，搜索引擎如此做

Posted on Edited on In Valine:

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。

你可以假设树和k都存在，并且1≤k≤树的总结点数。

样例
输入：root = [2, 1, 3, null, null, null, null] k = 3

输出：3

实现思路

首先，我们需要有一个认知：二叉搜索树等同于一个有序数组。

然后基于上面的认知去思考：我如何在一个有序数组中找到第k小的元素。

所以，我们需要中序遍历BST，在遍历过程中对访问的元素进行计数即可，当计数到k时，便是我们要找的元素。

这里科普一个常识：对于BST，我们一定是中序遍历！否则就浪费了BST有序的特性了。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int k;
    TreeNode* dfs(TreeNode* root) {
        if (root->left) {
            auto r = dfs(root->left);
            if (r) return r;
        }
        if (--k == 0) return root;

        if (root->right) return dfs(root->right);
        return nullptr;
    }

    TreeNode* kthNode(TreeNode* root, int _k) {
        k = _k;
        return dfs(root);    
    }
};

Posted on Edited on Valine:

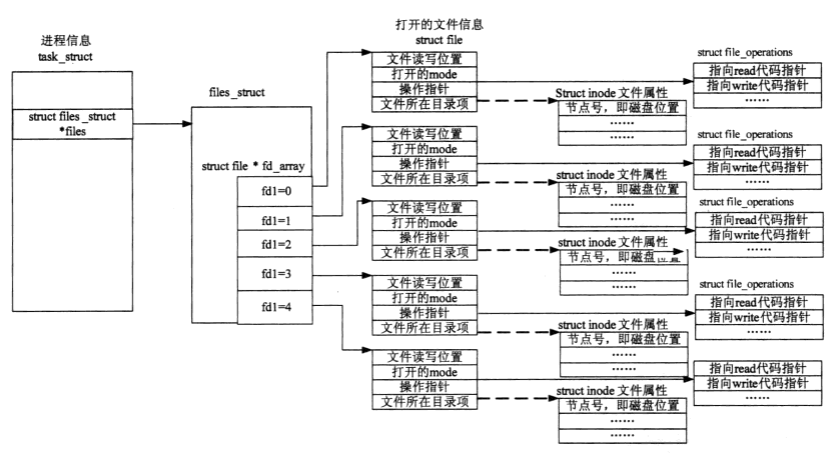
fd-inode

linux内核会为每一个进程创建一个task_truct结构体来维护进程信息，称之为 进程描述符，该结构体中 指针

struct files_struct *files

指向一个名称为file_struct的结构体，该结构体即 进程级别的文件描述表。

它的每一个条目记录的是单个文件描述符的相关信息

系统级别的文件描述符表
内核对系统中所有打开的文件维护了一个描述符表，也被称之为 【打开文件表】，表格中的每一项被称之为 【打开文件句柄】，一个【打开文件句柄】 描述了一个打开文件的全部信息。
主要包括：

当前文件偏移量（调用read()和write()时更新，或使用lseek()直接修改）
打开文件时所使用的状态标识（即，open()的flags参数）
文件访问模式（如调用open()时所设置的只读模式、只写模式或读写模式）
与信号驱动相关的设置
对该文件i-node对象的引用
文件类型（例如：常规文件、套接字或FIFO）和访问权限
一个指针，指向该文件所持有的锁列表
文件的各种属性，包括文件大小以及与不同类型操作相关的时间戳

Inode表
每个文件系统会为存储于其上的所有文件(包括目录)维护一个i-node表，单个i-node包含以下信息：

文件类型(file type)，可以是常规文件、目录、套接字或FIFO
访问权限
文件锁列表(file locks)
文件大小
等等
i-node存储在磁盘设备上，内核在内存中维护了一个副本，这里的i-node表为后者。副本除了原有信息，还包括：引用计数(从打开文件描述体)、所在设备号以及一些临时属性，例如文件锁。

为什么inode中没有文件名？

目录，也是文件。 文件内容是一个列表，列表项为：文件名 + inode

Posted on Edited on In Valine:

在Java语言中，可作为GC Roots的对象包含以下几种：

虚拟机栈(栈帧中的本地变量表)中引用的对象。(可以理解为:引用栈帧中的本地变量表的所有对象)
方法区中静态属性引用的对象(可以理解为:引用方法区该静态属性的所有对象)
方法区中常量引用的对象(可以理解为:引用方法区中常量的所有对象)
本地方法栈中(Native方法)引用的对象(可以理解为:引用Native方法的所有对象)

可以理解为:

(1)首先第一种是虚拟机栈中的引用的对象，我们在程序中正常创建一个对象，对象会在堆上开辟一块空间，同时会将这块空间的地址作为引用保存到虚拟机栈中，如果对象生命周期结束了，那么引用就会从虚拟机栈中出栈，因此如果在虚拟机栈中有引用，就说明这个对象还是有用的，这种情况是最常见的。

(2)第二种是我们在类中定义了全局的静态的对象，也就是使用了static关键字，由于虚拟机栈是线程私有的，所以这种对象的引用会保存在共有的方法区中，显然将方法区中的静态引用作为GC Roots是必须的。

(3)第三种便是常量引用，就是使用了static final关键字，由于这种引用初始化之后不会修改，所以方法区常量池里的引用的对象也应该作为GC Roots。最后一种是在使用JNI技术时，有时候单纯的Java代码并不能满足我们的需求，我们可能需要在Java中调用C或C++的代码，因此会使用native方法，jvm内存中专门有一块本地方法栈，用来保存这些对象的引用，所以本地方法栈中引用的对象也会被作为GC Roots。

先通过gc-root可达性分析给对象标记，然后执行finalize() 再给对象一次机会。

1、CMS

CMS(Concurrent Mark Sweep)，我们可以轻易地从命名上看出，它是一个并发的，然后是基于标记——清理的垃圾回收器，它清理垃圾的步骤大致分为四步：

初始标记（标记GCRoot能够关联到的对象）
并发标记（
重新标记
并发清理(会产生浮动垃圾)

初始标记只要是找到GC Roots，所以是一个很快的过程，并发标记和用户线程一起，通过GC Roots找到存活的对象，重新标记主要是修复在并发标记阶段的发生了改变的对象，这个阶段会Stop the World；

并发清理则是保留上一步骤标记出的存活对象，清理掉其他对象，正因为采用并发清理，所以在清理的过程中用户线程又会产生垃圾，而导致浮动垃圾，只能通过下次垃圾回收进行处理；

因为cms采用的是标记清理，所以会导致内存空间不连续，从而产生内存碎片

此处要清楚，CMS的垃圾回收的内存模型还是以我们常用的新生代，老年代的结构，如下图所示：

2.G1

G1(Garbage-First)，以分而治之的思想将堆内存分为若干个等大的Region块，虽然还是保留了新生代，老年代的概念，但是G1主要是以Region为单位进行垃圾回收，G1的分块大体结果如下图所示：

G1垃圾回收器的它清理垃圾的步骤大致分为四步：

初始标记
并发标记
最终标记
复制回收

初始标记和并发标记和CMS的过程是差不多的，最后的筛选回收会首先对各个Region的回收价值和成本进行排序，根据用户所期望的GC停顿时间来制定回收计划

因为采用的标记——整理的算法，所以不会产生内存碎片，最终的回收是STW的，所以也不会有浮动垃圾，Region的区域大小是固定的，所以回收Region的时间也是可控的

同时G1 使用了Remembered Set来避免全堆扫描，G1中每个Region都有一个与之对应的RememberedSet ，在各个 Region 上记录自家的对象被外面对象引用的情况。当进行内存回收时，在GC根节点的枚举范围中加入RememberedSet 即可保证不对全堆扫描也不会有遗漏。

Posted on Edited on In Valine:

N选K组合（无重复版）

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

N选K组合解题思路

状态：第i个

选择: n-i个选择

路径：path选择

结果集：列表

结束条件： 找到所有的组合； path路径到了k

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

// u 没有实际作用，可以通过path来替代；
vector<int> path;
void dfs(int u, int start_idx) {
    if (u == k) {
        //path
        return;
    }

    //未剪枝版
    for (int i = start_idx; i <= n; ++i) {
        path.push_back(i);
        dfs(u + 1, i + 1) ; //注意i+1
        path.pop_back();
    }

    //带剪枝版(如果i过大的话，剩下的元素会不足k个)
    for (int i = start_idx; i <= n - (k - path.size()); ++i) {
        path.push_back(i);
        dfs(u + 1, i + 1);
        path.pop_back();
    }

}

dfs(0, 0);

和为n的K个数的组合

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

N选K组合的和解题思路

状态：第i个

选择: 9-i个选择

路径：path选择

结果集：列表

结束条件： 找到所有的组合； path路径到了k，sum ok

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

vector<int> path;
void dfs(int u, int sum, int start) {
    if (sum > n) {return;}
    if (u == k) {
        if (sum == 0) {
            res.push_back(path);
        }
        return;
    }

    for (int i = start; i <= 9 - (k - path.size()) + 1; i++) {
        path.push_back(i);
        dfs(u + 1, sum - i, i + 1);
        path.pop_back();
    }
}

dfs(0, n, 0);

和为N的组合（无限选取版）

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。

解集不能包含重复的组合。

candidates找和为target解题思路

状态：第i个

选择: 每次都有N个选择

路径：path选择

结果集：列表

结束条件： 找到所有的组合； path路径到了k，sum ok

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//如果是一个集合来求组合的话，就需要startIndex
void dfs(vector<int>& d, int u, int sum, int start) {
    if (sum > target) {return;}
    if (sum == target) {
        res.push_back(path);
        return;
    }

    for (int i = start; i < n; ++i) {
        path.push_back(d[i]);
        dfs(d, u + 1, sum + d[i], i); //可以重复使用,
        path.pop_back();
    }
}

//剪枝优化： 排序(从大到小排序），提前终止，判定条件
void dfs(vector<int>& d, int u, int sum, int start) {
    if (sum > target) {return;}
    if (sum == target) {
        res.push_back(path);
        return;
    }

    //排序后，可以剪枝，提前终止本层（因为后面的更小了，只要i不可以，后面的更不可以，可以提前终止）
    for (int i = start; i < n && sum+d[i] <= target; ++i) {
        path.push_back(d[i]);
        dfs(d, u + 1, sum + d[i], i); //可以重复使用
        path.pop_back();
    }
}

和为N的组合（有重复，仅用一次）

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。

说明：
所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

//需要进行排序预处理，从大到小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dfs(vector<int>& d, int u, int sum, int start_index) {
        if (sum > target) {return;}
        if (sum == target) {
            res.push_back(path);
            return;
        }

        for (int i = start_index; i < n && sum + d[i] <= target; ++i) {
            //在同一层次上，相同的元素不重复选取（因为前面的已经处理过了）
            if (i >= 1 && d[i] == d[i - 1] && used[i - 1] == false) {continue;}
            path.push_back(d[i]);
            used[i] = true;
            dfs(d, u + 1, sum + d[i], i + 1);
            used[i] = false;
            path.pop_back();
        }
    }

所有数字的排列（无重复版）

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

解法1 给坑u找元素i

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void dfs(vector<int>& d, int u) {
    if (u == n) {
        res.push_back(path);
        return;
    }

    for (int i = 0; i < n; ++i ) {
        if (used[i]) continue;
        path.push_back(d[i]);
        //path[u] = nums[i]; 这样子其实也可以，这样子反而不需要还原现场；因为u的设置顺序是从大到小
        used[i] = true;
        dfs(d, u + 1);
        used[i] =false;
        path.pop_back();
    }
}

解法2: 特定元素(u)选择坑位（i)

//后面可以选择的坑原来越少了； u是第一个元素；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    
    void dfs(vector<int>& nums, int u, int state) {
        if (u == int(nums.size())) {
            res.push_back(path);
            return;
        }
        
        for (int i = 0; i < nums.size(); ++i) {
            if (!(state >> i & 1)) {
                //这一步骤是关键，为第u号元素找可以选择的坑位
                path[i]= nums[u];
                dfs(nums, u + 1, state + (1 << i));
            }
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        path.resize(nums.size());
        sort(nums.begin(), nums.end());
        dfs(nums, 0, 0, 0);
        return res;
    }
};

注意到前面的state与path的配合使用，有两个目的：保存当前坑位存了哪些元素了，保存坑位的使用情况。
有没有什么手段呢？ path可以d来替代；d的前半部分作为坑使用，后半部分保持原功能； 但是坑占用之前，需要保存其原值，一举两得。所以就有了下面这种解法。

    //u代表元素。
    void dfs(vector<int>& d, int u) {
        if (u == n) {
            res.push_back(d);
            return;
        }

        //这一步骤是关键，为第u号元素找可以选择的坑位
        for (int i = u; i < n; ++i ) {
            swap(d[u], d[i]);   //将u元素放入i号坑。
            dfs(d, u + 1);  
            swap(d[u], d[i]);
        }
    }

所有数字的排列（数字重复）

输入一组数字（可能包含重复数字），输出其所有的排列方式。

样例
输入：[1,2,3]

输出：
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

为坑（u）选择合适的元素（i）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//sort first
void dfs(int u) {
    if (u == nums.size()) {
        res.push_back(path);
        return;
    }
    for (int i = 0; i < nums.size(); i++) {
        if (i > 0 &&  nums[i] == nums[i - 1] && !used[i - 1]) continue; //两次访问，第一次访问是used[i-1]=true,会加到path中; 第二次访问used[i-1]=false，会被跳过。
        if (used[i]) continue;
        used[i] = true;
        //为新的坑，选择了一个新的元素
        path.push_back(nums[i]);
        dfs(u + 1);
        path.pop_back();
        used[i] = false;
    }
}

特定元素(u)选择坑位（i)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    
    void dfs(vector<int>& nums, int u, int start, int state) {
        if (u == int(nums.size())) {
            res.push_back(path);
            return;
        }
        
        //对于重复元素，则放在前面的元素后面；否则从0开始
        if (!u || nums[u] != nums[u - 1]) start = 0;
                
        for (int i = start; i < nums.size(); ++i) {
            if (!(state >> i & 1)) {
                //这一步骤是关键，为第u号元素找可以选择的坑位[i]
                path[i]= nums[u];
                dfs(nums, u + 1, i + 1, state + (1 << i));
            }
        }
    }
    
    vector<vector<int>> permutation(vector<int>& nums) {
        path.resize(nums.size());
        sort(nums.begin(), nums.end());
        dfs(nums, 0, 0, 0);
        return res;
    }
};

所有递增子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7] 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

解题思路

  1. 因为找到是递增子序列，所以不能排序；也就不能通过排序来去重了
  2. 可以考虑用hash_map来做去重。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dfs(int u, int start) {
       if (u >= 2) {
           res.push_back(path);
           //这里是不可以return的
       }

       unordered_set<int> iset;
       for (int i = start; i < d.size(); i++) {
           if (iset.count(d[i])) continue;
           if (path.size() && path.back() > d[i]) continue;

           iset.insert(d[i]);
           path.push_back(d[i]);
           dfs(u + 1, i + 1);
           path.pop_back();
       }
   }

https://zhuanlan.zhihu.com/p/339849416